Inerzia
Se si osserva un corpo in quiete rispetto, ad esempio, alla Terra, si osserva che tende a mantenere il suo stato, a meno che non intervenga qualcosa che lo fa muovere.
Apparentemente sembra non valere per un corpo in movimento: prima o poi si ferma. In realtà questo succede perché interviene, per esempio, l'attrito che lo frena.
L'inerzia è la tendenza di un corpo a mantenere il proprio stato di quiete o di moto rettilineo uniforme.
Principio di Inerzia di Leonardo da Vinci. Ogni corpo tende a conservare il proprio stato di quiete o di moto rettilineo uniforme finché non interviene una causa esterna a modificare tale stato.
Questo è anche il primo principio della dinamica, che riprenderemo nella pagina successiva.
Se appoggiamo su un pilastrino una lamina rigida con sopra una sfera pesante, colpendo la lamina, questa si allontana lasciando ferma la sfera. La lamina, se fosse libera nello spazio, senza che ci sia qualcosa né ostacoli il movimento, continuerebbe ad allontanarsi con moto rettilineo uniforme.

Lo stesso lo possiamo sperimentare se ci troviamo in piedi su un autobus. Quando parte, tendiamo a cadere all'indietro e quando frena, siamo spinti in avanti.
Forza
La causa che mantiene ferma la sfera della figura sopra e che fa allontanare la lamina si chiama forza.
La forza è la causa che produce un moto in un corpo in quiete, che modifica la costanza del vettore velocità o che deforma il corpo al quale è applicata.
Se un corpo è libero, sottoposto a una forza, si muove o varia il suo moto (effetto dinamico).
Se il corpo è vincolato, l'azione di una forza si riduce a una pressione o a una tensione esercitata sul corpo stesso, inducendo una deformazione più o meno rilevante (effetto statico).
La forza è una grandezza vettoriale e come tale è rappresentata da un segmento orientato, caratterizzato da intensità, direzione, verso e punto di applicazione.

L'unità di misura della forza nel SI è il newton N.
Lo strumento per misurare la forza è il dinamometro, costituito da una molla di acciaio con un indice all'estremità. Applicando una forza alla molla, questa si allunga e il valore si legge su una scala graduata.
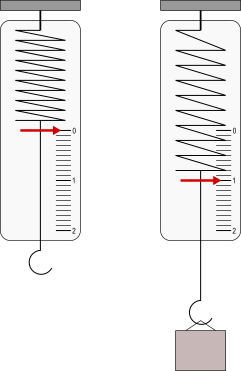
Un corpo si trova generalmente sottoposto all'azione di più forze contemporaneamente (sistema di forze), dette componenti.
La composizione delle forze consiste nel determinare un'unica forza equivalente (che produce lo stesso effetto) a tutte le forze componenti applicate insieme, detta risultante .
L'operazione inversa è la scomposizione.
Si definisce forza equilibrante di un sistema di forze quella forza che ha la stessa intensità e la stessa retta d'azione ma verso opposto della risultante ed è la forza da applicare a un corpo affinché sia in equilibrio.
Forze applicate a uno stesso punto
Le forze, in quanto vettori, si possono comporre secondo le regole illustrate nella pagina sulle operazioni sui vettori, a cui si rimanda.
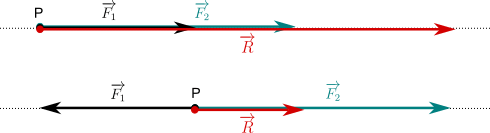
Forze con uguale direzione (collineari)
La risultante è una forza con la stessa direzione, intensità uguale alla somma o alla differenza vettoriale delle intensità delle componenti, secondo il verso concorde o discorde.
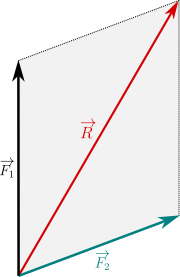
Forze con direzioni ad angolo (concorrenti)
La risultante si ricava mediante la regola del parallelogramma.
Forze con uguale direzione e intensità ma verso opposto
La risultante è nulla e tra loro si fanno equilibrio.

Forze applicate a punti diversi di un corpo rigido
Immaginiamo qui un corpo rigido perché le forse applicate producono sempre una deformazione.
Ribadiamo un principio enunciato parlando dei vettori: una forza può essere spostata lungo la retta d'azione (o di applicazione).
Date queste premesse forniamo un breve elenco delle possibili situazioni.
Forze opposte
Applichiamo due forze opposte in due punti di applicazione lungo la medesima retta d'azione. Spostando una delle sue forze nel punto di applicazione dell'altra, abbiamo un equilibrio. È il caso illustrato nel paragrafo precedente.

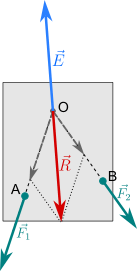
Forze convergenti
Applichiamo due forze diverse le cui rette di applicazione convergano in un punto. Spostando le due forze lungo le rispettive rette d'azione fino al punto di convergenza, troviamo la risultante applicando la regola del parallelogramma. In azzurro la forza equilibrante.
Forze parallele con lo stesso verso (cospiranti)
Applicando alle estremità di un'asta rigida due forze parallele e dello stesso verso (concordi), la risultante è una forza che ha come intensità la somma delle intensità, ha lo stesso verso e il punto di applicazione è all'interno dell'asta. Questo la divide in due parti inversamente proporzionali alle intensità delle componenti. In rosso la risultante, in azzurro la forza equilibrante.
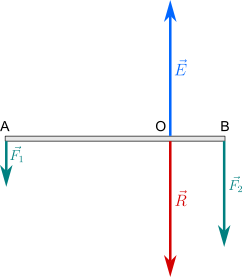
È possibile calcolare graficamente il punto di applicazione scambiando la posizione delle due forze e invertendone una. Il segmento che congiunge le due nuove forze, intersecando l'asta, individua il punto di applicazione.
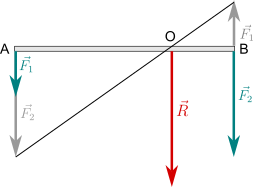
Forze parallele diseguali con versi opposti
Impostazione come il caso precedente, ma le forze hanno verso opposto (discordi) e sono di intensità diversa. La risultante ha come intensità la differenza delle intensità, il verso della maggiore e il punto di applicazione esterno all'asta tale che la sua distanza da essi sia inversamente proporzionale all'intensità delle componenti. In azzurro la forza equilibrante.

Con lo stesso metodo del caso precedente possiamo determinare graficamente il punto di applicazione.

Coppia
Si ha la coppia quando a un corpo rigido sono applicate, in punti diversi non aventi la stessa retta d'azione, due forze parallele di uguale intensità e di verso opposto. In questo caso, non si ha risultante, ma il corpo ruota finché le due forze non vengono a trovarsi sulla stessa retta d'azione.
La distanza tra le rette d'azione delle due forze si chiama braccio b.
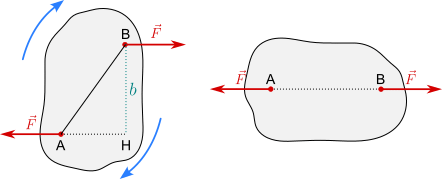
Al termine della rotazione b = 0.
L'effetto rotatorio è misurato da una nuova grandezza scalare, chiamata momento.
Il momento è un vettore che descrive l'attitudine di un sistema a ruotare attorno a un asse. La rotazione dipende quindi dal momento e non dalla forza in sé.
Il momento scalare M di una coppia è dato dal prodotto dell'intensità della forza F per il braccio b ed è direttamente proporzionale sia all'intensità della forza, sia al braccio.
Il momento si misura in newton metro (N∙m).
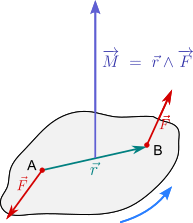
Per conoscere il senso di rotazione del corpo è necessario introdurre un vettore, chiamato vettore momento o vettore assiale. Questo ha direzione perpendicolare al piano delle due forze, verso quello dai piedi alla testa di un osservatore posto ritto sul piano della coppia vede la rotazione svolgersi in senso antiorario (oppure con uno dei metodi visti qui), intensità uguale a quella del momento scalare e punto di applicazione che può trovarsi in un punto qualsiasi dello spazio (vettore libero).
La formula del momento vettoriale è la seguente:
dove è il vettore che congiunge A e B.
Massa e peso
Nel linguaggio comune si usano a volte i termini massa e peso come sinonimi e quindi intercambiabili. Si tratta invece di due concetti diversi.
Massa
La massa è una grandezza scalare che indica la quantità di materia di un corpo ed è una proprietà intrinseca del corpo stesso, che non varia durante il moto ed è indipendente dal luogo di misurazione e dalle forze a cui il corpo può essere sottoposto.
Poiché la materia è costituita da atomi e ciascun atomo ha una propria massa costante, mai nulla, la massa del corpo è data dalla somma delle masse di tutti gli atomi che lo compongono.
Più precisamente, la massa misura l'inerzia di un corpo, cioè la resistenza che oppone a una forza che tende a modificare il suo stato di quiete o di moto. Per questo è definita massa inerziale.
Quanto maggiore è la massa di un corpo, tanto maggiore è la forza che dobbiamo impiegare per spostarlo.

Per misurare la massa di un oggetto si usa una stadera (bilancia a un piatto), che funziona con il principio della leva (vedi più sotto), dove abbiamo una sola massa campione che scorre su un'asta, oppure una bilancia a due piatti e due bracci uguali. Su un piatto si mette l'oggetto da massare, mentre sull'altro si aggiungono progressivamente delle masse campione finché non si raggiunge l'equilibrio.
In alternativa si può adoperare una particolare bilancia digitale, che usi lo stesso principio.
Il luogo dove viene effettuata la misurazione è indifferente perché si confronta la massa del corpo e non il peso.

La massa misurata con la bilancia non è la massa inerziale, ma la massa gravitazionale perché misura l'attrazione gravitazione, che è identica nei due piatti.
La massa inerziale e la massa gravitazionale sono equivalenti, ma per trovarne la spiegazione bisogna ricorrere al principio di equivalenza della teoria della relatività.
Nel SI la massa è una grandezza fondamentale la cui unità è il chilogrammo kg. La massa campione è un cilindro di platino-iridio di 1 Kg-massa conservato al Bureau International des Poids et Mesures a Sèvres, in Francia.
Peso
Un corpo, se non appoggiato o sostenuto, cade a terra. Questo è apparentemente in contraddizione al principio di inerzia, per cui il corpo dovrebbe mantenere il suo stato di quiete. In realtà esiste una forza che lo fa cadere: è la gravità.
Tutti i corpi presenti sulla Terra (o su qualsiasi corpo celeste) sono attirati verso il suo centro dalla forza di gravità.
La forza di gravità, o forza-peso, detta comunemente peso, è una grandezza vettoriale che dipende dall'accelerazione di gravità.
L'accelerazione di gravità è un vettore con direzione perpendicolare alla superficie terrestre, senso rivolto verso il basso e intensità variabile secondo il luogo considerato. Sulla Terra, a livello del mare, è circa uguale a 9,8 m/s2 (sulla Luna è 1,6 m/s2).
Il peso rappresenta perciò la forza gravitazionale con la quale un corpo (grave), in quanto dotato di massa, è attratto verso il centro Terra (o altro corpo celeste).
Ricordiamo che in realtà anche il corpo esercita un'attrazione gravitazionale nei confronti della Terra, secondo la legge della gravitazione universale di Newton ma, essendo la massa del primo infinitesima rispetto alla seconda, può essere trascurata.
La relazione che lega la massa alla forza-peso è la seguente:
Si noti come massa e peso siano direttamente proporzionali e l'accelerazione di gravità è la costante di proporzionalità. Questo significa che, in uno stesso luogo, corpi di massa uguale hanno peso uguale.
Il vettore ha come direzione la verticale del luogo, il senso è diretto verso il centro della Terra (o altro corpo celeste), intensità pari al “peso” (kg-peso) e il punto di applicazione è il centro del corpo (centro di gravità o baricentro).
Mentre la massa è costante e non può essere nulla, il peso varia in base alla forza di gravità, perciò può anche essere nullo se il corpo si trova lontano da qualsiasi oggetto celeste e non risente di alcuna attrazione gravitazionale.
Anche sulla Terra stessa il peso non è identico in ogni punto della superficie. Infatti, avendo la forma del geoide, il peso è inferiore dove la superficie si innalza perché il grave è più lontano dal centro della Terra, e viceversa. Dipende quindi dall'altitudine e dalla latitudine.
Il peso si misura con il dinamometro, che abbiamo presentato sopra, o con una “bilancia” pesapersone, che in realtà è un dinamometro, in cui viene rilevata la deformazione di una molla.

L'unità di misura del peso nel SI è, come per le altre forze, il newton N, una grandezza derivata del SI.
Nella pratica quotidiana non si usa il N come unità di misura. Sarebbe spiazzante per un fruttivendolo sentirsi chiedere 10 N di patate.
Per questo si usa comunemente il chilogrammo o, più precisamente, il chilogrammo-peso, definito come la forza con cui nel vuoto, alla latitudine di 45°, è attratto dalla Terra il cilindro campione.
Poiché il valore medio di sulla superficie terrestre è 9,8 m/s2, il peso di un corpo di massa di 1 Kg è uguale a 9,8 N:
1 kgpeso = 1kgmassa × 9,8 m/s2 = 9.8 N
Supponiamo di voler valutare la massa e il peso di una ragazza sulla Terra e sulla Luna usando rispettivamente una bilancia e un dinamometro.
Se la ragazza sulla Terra “pesa” 60 kg (nel linguaggio comune), significa che ha:
- massa = 60 kg
- peso = 60 kg × 9,8 m/sec2 = 588 N
Sulla Luna ha:
- massa = 60 kg
- peso = 60 kg × 1,6 m/sec2 = 96 N
Come si vede, la massa della ragazza non è cambiata ma il peso si è ridotto di ⅙.
Nella figura seguente, per esigenze grafiche, di chiarezza e semplicità abbiamo usato sempre il Kg.

- LE FORZE DELLA NATURA
Tutti i fenomeni che si verificano nell'Universo, sia a livello microscopico (molecole, atomi, nuclei atomici), sia a livello macroscopico (pianeti, stelle, galassie) sono descritti da leggi della meccanica classifica fino alla quantistica, basandosi su 4 forze fondamentali. Più correttamente, si deve parlare di interazioni fondamentali perché agiscono in coppia, cioè si scambiano particelle mediatrici durante la loro azione.
In ordine di intensità crescente, le 4 interazioni sono: gravitazionale, nucleare debole, elettromagnetica, nucleare forte. Tra la prima e l'ultima c'è una differenza di intensità di miliardi di volte.
Un'altra differenza riguarda il raggio d'azione. Alcune, come la gravità fanno sentire i loro effetti a distanze enormi mentre altre interagiscono solo quando le particelle sono vicinissime tra loro.
Infine, alcune forze sono solo attrattive mentre altre sono sia attrattive, sia repulsive.Interazione gravitazionale
 L'interazione gravitazionale, quella che noi conosciamo come forza di gravità, o semplicemente gravità, è una forza sempre attrattiva che si esercita tra particelle dotate di massa. È la più debole tra le forze fondamentali, ma a livello macroscopico è quella che definisce la struttura dell'Universo anche a grandissima distanza. Da questa forza dipende, l'aggregazione di particelle per formare i diversi corpi celesti, il moto dei pianeti attorno alle stelle, le relazione tra le stelle all'interno delle galassie e i rapporti tra le galassie nell'Universo. A distanze inferiori, il peso dei corpi che si trovano sulla Terra (o altro corpo celeste) è la forza di gravità esercitata su di essi dal nostro pianeta. Per esempio, una pietra posta sopra una palla di gomma la deforma, il che significa che la pietra esercita una forza dovuta all'attrazione terrestre.
L'interazione gravitazionale, quella che noi conosciamo come forza di gravità, o semplicemente gravità, è una forza sempre attrattiva che si esercita tra particelle dotate di massa. È la più debole tra le forze fondamentali, ma a livello macroscopico è quella che definisce la struttura dell'Universo anche a grandissima distanza. Da questa forza dipende, l'aggregazione di particelle per formare i diversi corpi celesti, il moto dei pianeti attorno alle stelle, le relazione tra le stelle all'interno delle galassie e i rapporti tra le galassie nell'Universo. A distanze inferiori, il peso dei corpi che si trovano sulla Terra (o altro corpo celeste) è la forza di gravità esercitata su di essi dal nostro pianeta. Per esempio, una pietra posta sopra una palla di gomma la deforma, il che significa che la pietra esercita una forza dovuta all'attrazione terrestre.
A livello microscopico, invece, i suoi effetti sono trascurabili.
La legge della gravitazione di Newton (1687) ci dice che la forza gravitazionale è direttamente proporzionale alle masse in gioco e diminuisce rapidamente con la distanza dai centri di massa (vedi la sez. Astronomia). Secondo Einstein, invece, la gravità non è una forza ma una deformazione dello spazio-tempo (vedi la sez. Tempo).
Tra le quattro forze, questa è l'unica di cui non si sia ancora individuata la particella mediatrice, il gravitone, un'ipotetica particella di massa nulla che viaggerebbe alla velocità della luce.Interazione nucleare debole
 L'interazione nucleare debole, la cui intensità è però superiore alla precedente, è responsabile di tutti quei fenomeni riguardanti la radioattività (vedi par. Radioattività), il decadimento di isotopi instabili in particelle più stabili (vedi par. Datazioni radiometriche), l'emissione di particelle α, β, γ e raggi X, la trasformazione di neutroni in protoni ed elettroni, le reazioni di fusione nucleare all'interno delle stelle.
L'interazione nucleare debole, la cui intensità è però superiore alla precedente, è responsabile di tutti quei fenomeni riguardanti la radioattività (vedi par. Radioattività), il decadimento di isotopi instabili in particelle più stabili (vedi par. Datazioni radiometriche), l'emissione di particelle α, β, γ e raggi X, la trasformazione di neutroni in protoni ed elettroni, le reazioni di fusione nucleare all'interno delle stelle.
Si tratta di una forza sempre attrattiva il cui raggio d'azione è limitato a livello subatomico.
Le particelle responsabili di questa interazione sono i bosoni W± e Z0, scoperti da Carlo Rubbia e Simon van der Meer nel 1984.Interazione elettromagnetica
 L'interazione elettromagnetica, più forte della precedente, unisce il comportamento elettrico, dovuto alla presenza di cariche elettriche, a quello magnetico, causato dal movimento di queste. Agisce, quindi tra particelle dotate di carica elettriche, come i protoni e gli elettroni. Se le cariche sono di segno opposto si attraggono, mentre se sono dello stesso segno si respingono.
L'interazione elettromagnetica, più forte della precedente, unisce il comportamento elettrico, dovuto alla presenza di cariche elettriche, a quello magnetico, causato dal movimento di queste. Agisce, quindi tra particelle dotate di carica elettriche, come i protoni e gli elettroni. Se le cariche sono di segno opposto si attraggono, mentre se sono dello stesso segno si respingono.
Da questa forza, attrattiva o repulsiva, dipende la forma e lo stato della materia, poiché tiene uniti più o meno fortemente gli atomi tra le molecole e all'interno di queste gli atomi tra loro e ancora più all'interno gli elettroni intorno al nucleo atomico, dando origine alle proprietà chimiche e anche fisiche, come le forze di adesione e coesione. La rimozione di cariche elettriche negative strofinando il cappuccio di una penna biro su un panno di lana, produce un'attrazione elettrostatica su piccoli frammenti di carta e, su scala più grande, i fulmini. È quindi responsabile dei fenomeni elettrici - onde radio, attrito, contrazione muscolare, reazioni chimiche, ecc. - e anche magnetici. Da questa forza, infatti, dipende per esempio l'attrazione o la repulsione di poli magnetici nelle calamite.
Anche questa forza ha un raggio d'azione infinito come quella gravitazionale, ma l'intensità è maggiore.
Le particelle mediatrici di questa forza sono dei bosoni privi di massa, i fotoni.Interazione nucleare forte
 L'interazione nucleare forte, che può essere attrattiva o, a distanza inferiore, repulsiva, è ovviamente la più forte perché deve tenere uniti i neutroni e i protoni nel nucleo, impedendo che questi ultimi, avendo carica positiva, si respingano l'un l'altro. Tiene uniti anche i quark, le particelle che costituiscono i protoni e i neutroni. Il raggio d'azione deve essere estremamente piccolo, dovendo agire all'interno dei nuclei atomici, altrimenti prevarrebbero le forze repulsive tra cariche di uguale segno. Da notare che, rispetto alle altre forze, diventa più forte, anziché più debole, all'aumentare della distanza tra le particelle e questo impedisce ai quark di allontanarsi.
L'interazione nucleare forte, che può essere attrattiva o, a distanza inferiore, repulsiva, è ovviamente la più forte perché deve tenere uniti i neutroni e i protoni nel nucleo, impedendo che questi ultimi, avendo carica positiva, si respingano l'un l'altro. Tiene uniti anche i quark, le particelle che costituiscono i protoni e i neutroni. Il raggio d'azione deve essere estremamente piccolo, dovendo agire all'interno dei nuclei atomici, altrimenti prevarrebbero le forze repulsive tra cariche di uguale segno. Da notare che, rispetto alle altre forze, diventa più forte, anziché più debole, all'aumentare della distanza tra le particelle e questo impedisce ai quark di allontanarsi.
L'interazione forte si manifesta mediante bosoni privi di massa, chiamati gluoni, dotate di una carica non di tipo elettrico (colore).Unificare le forze
Da sempre gli scienziati hanno cercato la semplicità e l'eleganza formale delle leggi che governano la natura e questo vale anche per le forze fondamentali, provando a dimostrare che forze apparentemente diverse, sono in realtà manifestazioni differenti di una medesima forza.
La prima unificazione è stata fatta da Isaac Newton nel 1687, dimostrando che l'attrazione gravitazionale terrestre è la stessa che agisce anche tra i corpi celesti.
Michael Faraday e André-Marie Ampère nel 1830, e poi James Clerk Maxwell nel 1873, unificarono la forza elettrica e magnetica, considerandole componenti diverse della medesima forza, l'elettromagnetismo.
A energie molto elevate i fisici Sheldon Glashow, Steven Weinberg e Abdus Salam hanno vinto il Nobel nel 1979 per aver teorizzato l'unione tra l'interazione elettromagnetica e l'interazione debole per formare l'interazione elettrodebole e dimostrata da Carlo Rubbia e Simon van der Meer nel 1984 (premi Nobel).
Si pensa, anche ed è previsto teoricamente, che sia possibile unire l'interazione elettrodebole con quella forte per ottenere un'interazione elettronucleare.
Al momento resta fuori da quello che è definito Modello standard - un'unica teoria che riunisca tutte le forze e le particelle elementari - l'interazione gravitazionale.
Pressione
Quando la forza-peso, detta forza premente , è perpendicolare alla superficie e si esercita uniformemente su di essa, il valore del modulo della pressione p è dato dal rapporto tra l'intensità F della forza e l'area S della superficie cui è applicata.
Ne consegue che maggiore è la superficie, minore è la pressione.
L’unità di misura della pressione nel SI è il pascal (Pa), che corrisponde alla pressione esercitata dalla forza di un newton perpendicolare alla superficie di un m2.
Per i fluidi si usano anche altre unità di misura che vedremo nella sezione dedicata alla meccanica dei fluidi.
Prendiamo due tronchi di piramide a base quadrata identici (nella figura sono visti frontalmente), del peso di 1 kg ciascuno, con la base maggiore di 10 cm2 e quella minore di 6 cm2.
Il primo lo poggiamo con la base maggiore su una superficie elastica, mentre l’altro con la base minore.
La deformazione del primo sulla superficie elastica sarà inferiore a quella del secondo perché le pressioni (dopo la conversione) saranno rispettivamente:
(1 kg = 9,8 N)
- 9,8 N / 0,001 m2 = 9800 Pa
- 9,8 N / 0,0006 m2 = 16300 Pa

Equilibrio
L'applicazione di una forza a un corpo tende a farlo muovere. Poiché esistono corpi fermi, significa che le forze si fanno equilibrio oppure il corpo è appoggiato o sospeso.
Supponiamo che a un corpo libero siano applicate delle forze. Abbiamo visto in precedenza che tali forze possono essere composte trovando sempre una risultante che tende a spostarlo e una coppia che lo fa ruotare quindi:
Un sistema di forza applicate a un corpo libero è in equilibrio quando la risultante e il momento della coppia, equivalenti al sistema di forze date, sono entrambi nulli.
|
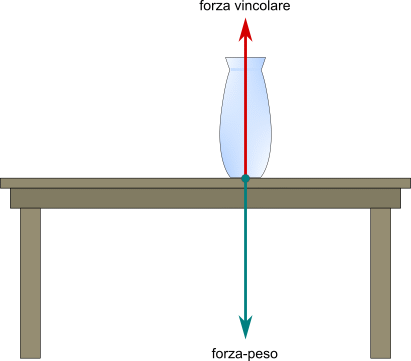
Un corpo è vincolato se può compiere solo movimenti che non siano incompatibili con il vincolo. Il vincolo è quindi un corpo fisso che impedisce a un altro corpo di compiere alcuni movimenti.
Nella figura, il vaso è sottoposto alla forza-peso che lo attira verso il basso ma non cade perché riceve una forza contraria (forza o reazione vincolare) opposta, diretta verso l'alto, dovuta al piano del tavolo (vincolo).
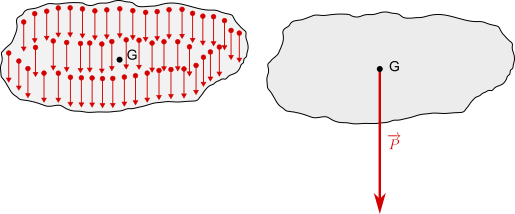
Baricentro
Ogni corpo è costituito da particelle elementari, ciascuna delle quali risente della forza di gravità. Se il corpo non è troppo esteso, le forze si possono considerare parallele, data l'enorme distanza rispetto al centro della Terra.
Componendo queste forze, si ottiene una risultate che avrà come modulo la somma dei moduli delle singole particelle - che è il peso del corpo -, direzione passante per il centro terrestre, senso verso il basso e punto di applicazione applicato al centro delle forze parallele, chiamato baricentro o centro di gravità G.
Equilibrio di gravi liberi e vincolati
Grave libero
Un grave libero può essere mantenuto in equilibrio applicando una forza uguale e contraria alla forza-peso , chiamata forza o reazione vincolare
, tale che la sua retta d'azione coincida con la verticale passante per il suo baricentro.

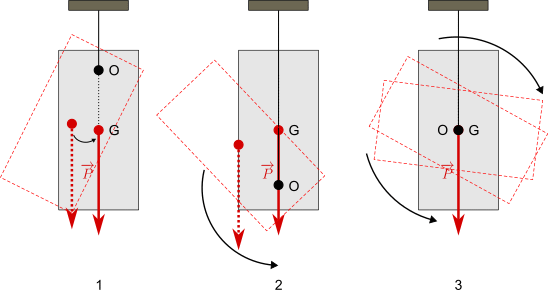
Grave sospeso a un punto
Un grave sospeso a un punto (vincolato) è in equilibrio quando ha momento nullo rispetto al punto di sospensione e il suo baricentro giace sulla verticale passante per il punto di sospensione.
Considerando che il baricentro tende ad assumere la posizione più bassa possibile, si possono presentare tre situazioni.
- Se il punto di sospensione O si trova sopra il baricentro G, abbiamo equilibrio stabile perché il corpo, anche se viene spostato, ritorna spontaneamente nella sua posizione.
- Se il punto di sospensione O si trova sotto il baricentro G, abbiamo equilibrio instabile perché il corpo, a un piccolo spostamento, ruota finché il baricentro non viene a trovarsi sotto il punto di sospensione.
- Se il baricentro G e il punto di sospensione coincidono, si ha equilibrio indifferente perché a ogni spostamento il corpo non torna più alla sua posizione iniziale, ma assume una nuova posizione, sempre in equilibrio.
Grave appoggiato
Un corpo pesante appoggiato a un piano orizzontale è in equilibrio quando la verticale al piano passante per il baricentro cade all'interno della base del grave. Di conseguenza, quanto più la base è ampia, tanto più il corpo è in equilibrio stabile.
Inoltre, tanto più il baricentro è in basso, tanto più è stabile.
Per avere l'equilibrio devono quindi essere rispettate due condizioni:
- la base d'appoggio deve essere la più ampia possibile;
- il baricentro del grave deve essere nella posizione più bassa possibile.
Immaginiamo un parallelepipedo snodabile, cioè in grado di piegarsi. Questo rimane in equilibrio finché la verticale che passa per il centro resta all'interno della base (a). Quando la verticale esce dalla base il parallelepipedo si capovolge.
Se abbassiamo il baricentro, la stabilità aumenta (b) e occorre inclinarlo molto per rovesciarlo.
Viceversa, se lo alziamo, la stabilità diminuisce (c) e basta poco per capovolgerlo.

Osserviamo ora i tre solidi della figura sottostante.
Il cubo (a) ha una base ampia e si trova in equilibrio stabile. Il cono (b), avendo una base ridottissima, si trova in equilibrio instabile, perciò cade. La sfera (c), invece, mantiene sempre la verticale passante per il baricentro all'interno e quindi si trova in un equilibrio indifferente.

Macchine semplici
Una macchina è un dispositivo che serve a equilibrare una forza (resistenza ) con un'altra di caratteristiche diverse (potenza
o forza motrice).
Una macchina può essere vantaggiosa, svantaggiosa o indifferente e questo è definito da un numero n, detto vantaggio statico, che si ottiene facendo il rapporto tra l'intensità della resistenza R e quella della potenza P.
Se P < R la macchina è vantaggiosa, se P = R è indifferente, se P > R è svantaggiosa.
Le macchine semplici, che sono dei meccanismi primitivi, sono state le prime a essere inventate e impiegate dall'uomo, con la funzione di amplificare le forze, permettendo di svolgere lavori impossibili con la sola forza muscolare.
Leva
La leva è formata da una barra rigida di peso trascurabile, in grado di ruotare attorno a un punto o a un asse fisso, detto fulcro. Le due forze e
, applicate alle estremità, agiscono perpendicolarmente all'asse di rotazione. Le loro distanze dal fulcro sono rispettivamente il braccio della potenza bP e il braccio della resistenza bR.
L'equilibrio si ha quando i momenti scalari della resistenza e della potenza rispetto al fulcro sono uguali e di segno opposto, quindi quando tendono a imprimere una rotazione in senso contrario,
MR = -MP
cioè quando il prodotto della potenza per il braccio della potenza è uguale al prodotto della resistenza per il braccio della resistenza:
PbP = RbR
In altri termini, si ha l'equilibrio quando resistenza e potenza e le loro intensità sono inversamente proporzionali ai rispettivi bracci:
Esistono tre tipi di leve.
- Leva di primo genere. La leva ha il fulcro tra la potenza e la resistenza. Questa leva è vantaggiosa se il braccio della potenza è maggiore di quello della resistenza; viceversa è svantaggiosa. Se i due bracci sono uguali, è indifferente. Il valore di n può essere quindi, maggiore, minore o uguale a 1. Esempi di leva vantaggiosa sono il piede di porco, la tenaglia, le forbici.

- Leva di secondo genere. La leva ha la resistenza tra il fulcro e la potenza. Questa leva è vantaggiosa perché il braccio della potenza è sempre maggiore del braccio della resistenza (n > 1). Ne sono esempi lo schiaccianoci, la carriola.

- Leva di terzo genere. La leva ha la potenza applicata tra il fulcro e la resistenza. Questa leva è sempre svantaggiosa, tuttavia indispensabile per compiere alcune azioni. Ad esempio abbiamo le pinzette, le molle per afferrare le braci, l'avambraccio, in cui il gomito è il fulcro, il muscolo è la potenza, mentre la resistenza è applicata alla mano.

Carrucola
La carrucola (o puleggia) è una macchina costituita da un disco rigido con una scanalatura dove scorre una fune, sostenuto da una staffa fissata a un gancio, che ruota attorno a un asse fisso (perno). Esistono due tipi di carrucole: fissa e mobile.
Carrucola fissa
Nella carrucola fissa la staffa è fissa a un sostegno mentre la resistenza (cioè la forza-peso del grave)* e la potenza
sono applicate direttamente nei punti A e B del bordo del disco, oppure alle estremità della fune. In pratica si comporta come una leva 1° genere a bracci uguali, con fulcro nel perno.
L'equilibrio si ha quando le intensità della resistenza e della potenza sono uguali e i momenti della resistenza e della potenza rispetto all'asse di rotazione hanno la stessa intensità ma verso opposto:
R = P MR = -MP
In questa carrucola n = 1, essendo entrambi i bracci uguali al raggio, perciò non è né vantaggiosa, né svantaggiosa. È una macchina che però è utile in diverse situazioni. Se, per esempio, voglio sollevare un secchio pesante (figura sotto), dovrei applicare una forza dal basso verso l'alto. Con l'uso della carrucola l'operazione è resa più agevole cambiando direzione e verso della forza.

* Per omogeneità con le altre macchine, usiamo
R
per indicare la forza-peso invece di
P
, riservando quest'ultima sempre alla potenza e non al peso.
Carrucola mobile
La carrucola mobile ha un capo della fune fissata a un sostegno mentre l'altro è sostenuto dalla potenza . La carrucola, con la fune inserita nella scanalatura, rimane mobile e alla staffa di questa è fissata la resistenza
.
Questa macchina si comporta come una leva di 2° genere, dove il fulcro (O) si trova a un estremo del disco, il braccio della potenza (OB) è il diametro e il braccio della resistenza (OA) è il raggio, perciò il primo è il doppio del secondo.
In questo caso, la resistenza è equamente ripartita tra i due capi della fune, quindi per equilibrarla è necessaria metà potenza.
Questa macchina, avendo n = 2, è sempre vantaggiosa ed è molto utilizzata in edilizia e in meccanica per sollevare pesi.

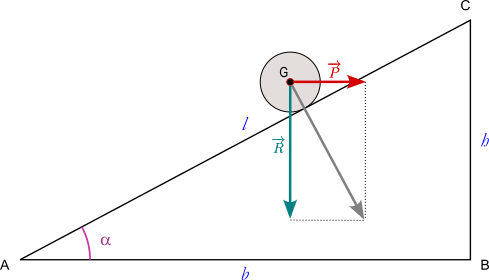
Piano inclinato
Il piano inclinato è una macchina formata da un piano liscio e rigido, costituente l'ipotenusa di un triangolo rettangolo, che forma un angolo α con il piano orizzontale (base del triangolo).
Un grave, che rappresenta la resistenza (cioè la forza-peso applicata al baricentro G) *, posto sul piano non rimane in equilibrio a causa del proprio peso e scivola in basso. Per avere l'equilibrio occorre applicare una potenza
.
Se la potenza è parallela alla lunghezza l, si ha l'equilibrio quando il rapporto tra le intensità della resistenza e della potenza è uguale al rapporto fra la lunghezza e l'altezza.
R : P = l : h
Lo possiamo visualizzare scomponendo il vettore lungo due direzioni, rispettivamente parallela e perpendicolare alla lunghezza.
Questa macchina è sempre vantaggiosa perché, essendo sempre h < l, sarà sempre P < R. Inoltre, è tanto più vantaggiosa quanto minore è la pendenza, cioè il rapporto h/l.

* Per omogeneità con le altre macchine, continuiamo usare
R
invece di
P
, indicando con quest'ultima, sempre la potenza e non il peso.
Se la potenza è parallela alla base b, si ha equilibrio quando resistenza e potenza sono direttamente proporzionali alla base e all'altezza.
R : P = b : h
Anche qui lo possiamo visualizzare scomponendo il vettore lungo due direzioni, rispettivamente parallela e perpendicolare alla base.
In questo caso il piano inclinato può essere vantaggioso o svantaggioso a seconda che α sia < o > di 45°, cioè se b è rispettivamente > o < di h.
Un'applicazione del piano inclinato la possiamo osservare nella funivia. Più in generale, è impiegato per spostare grossi pesi con uno sforzo inferiore rispetto al sollevamento verticale. Pensiamo a come vengono caricate le auto in una bisarca, oppure come gli antichi egizi sono riusciti a costruire le piramidi portando in alto enormi massi di pietra.


