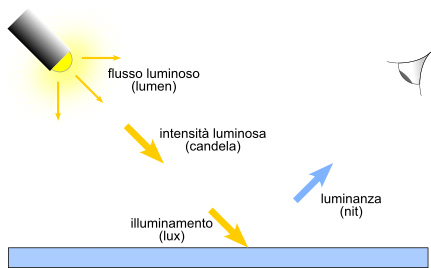
La fotometria è quel ramo dell'ottica che si occupa della misurazione della luce, cioè individua le grandezze fisiche che si riferiscono alla quantità di luce emessa da una sorgente, propagata nello spazio, ricevuta da una superficie.
Le grandezze fondamentali sono: intensità luminosa, flusso luminoso, luminanza, illuminamento.
Intensità luminosa
L'intensità luminosa fa riferimento alla luce emessa da una sorgente.
L'intensità luminosa di una sorgente è legata alla potenza emessa dalla sorgente, cioè alla quantità di energia emessa in 1 secondo, misurata in watt (W).
Questo però non è indicativo perché, per esempio, a parità di potenza una lampada a led ha un'intensità luminosa molto maggiore rispetto a una a filamento.
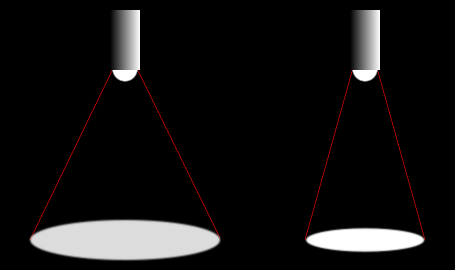
L'intensità luminosa I di una sorgente puntiforme S rappresenta la quantità di luce che la sorgente invia nell'unità di tempo in una data direzione, sull'unità di superficie della sfera di raggio unitario r, col centro nella sorgente stessa, entro l'angolo solido Ω.

L'intensità luminosa I è in relazione con un altro parametro, il flusso luminoso Ф, che vedremo qui di seguito.
Questa è data dal rapporto tra il flusso luminoso Ф e l'angolo solido Ω, secondo la relazione:
L'angolo solido si calcola dividendo l'area A della porzione di superficie sferica per il raggio della sfera al quadrato:
L'unità di misura nel SI è la candela (cd).
Due sorgenti che hanno lo stesso flusso luminoso possono avere intensità diversa secondo le dimensioni dell'angolo solido: più l'angolo del fascio luminoso è piccolo, maggiore è l'intensità della luce emessa.
Flusso luminoso
Il flusso luminoso fa riferimento alla luce trasmessa dalla sorgente.
Una sorgente puntiforme S, di intensità I, emette complessivamente una luce che si propaga nello spazio in tutte le direzioni, formando il flusso luminoso totale, indicato con Ф.
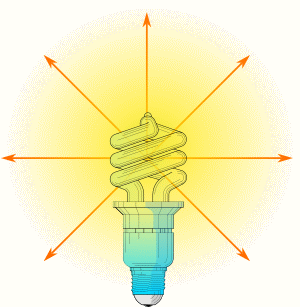
Il flusso luminoso nel SI si misura in lumen (lm): il flusso di 1 lumen viene emesso da una sorgente luminosa che ha, in ogni direzione, l'intensità di 1 candela.
Quantità luminosa
La quantità luminosa Q è il flusso luminoso totale che la sorgente S emette in 1 secondo.
La quantità luminosa si misura in lm/s.
Se invece di tutto lo spazio si considera solo lo spazio conico compreso entro l'angolo solido Ω col vertice nella sorgente stessa, la quantità di luce Q è data da:
Il flusso luminoso Q è la quantità di luce che la sorgente S emette in 1 secondo entro l'angolo solido Ω:
Illuminamento
L'illuminamento fa riferimento alla luce ricevuta da una superficie.
L'illuminamento E di una superficie con area A è il flusso luminoso di una sorgente di intensità I, in direzione perpendicolare, ricevuto dall'unità di tale superficie, cioè è dato dal rapporto tra il flusso ricevuto dalla superficie e l'area della superficie, misurata in m2.
L'illuminamento in pratica ci dice quanto la superficie viene illuminata e quindi più ampia è la superficie e minore è il flusso ricevuto.
Nel SI l'unità di misura è il lux, corrispondente a una sorgente di intensità luminosa di 1 cd, disposta perpendicolarmente alla direzione dei raggi luminosi, che illumina una superficie di 1 m2 posta alla distanza di 1 m.
Vediamo ora l'illuminamento in riferimento all'intensità I, servendoci della figura sotto.
Consideriamo una sorgente puntiforme S di intensità I emessa entro l'angolo solido Ω su una superficie perpendicolare alla direzione di propagazione, posta alla distanza r. Se L'angolo è molto piccolo, la superficie si può considerare piana e quindi ogni suo punto è equidistante dalla sorgente.
La legge di Lambert* afferma che l'illuminamento E su una superficie A perpendicolare ai raggi luminosi è direttamente proporzionale all'intensità luminosa I della sorgente e inversamente proporzionale al quadrato della distanza r della sorgente dalla superficie illuminata perciò, più ci si allontana dalla sorgente, più l'illuminamento della superficie diminuisce.

Se la superficie che riceve la luce non è perpendicolare alla direzione di propagazione, ma ha un angolo di incidenza α, l'illuminamento è minore e, sempre per la legge di Lambert, è direttamente proporzionale all'intensità luminosa e al coseno dell'angolo α compreso tra la direzione di incidenza della luce e la perpendicolare alla superficie e inversamente proporzionale al quadrato della distanza r tra la sorgente e la superficie:

Con α = 0 la formula diventa la prima.
Nella figura sotto possiamo vedere l'illuminamento in base all'incidenza dei raggi: massimo se i raggi sono perpendicolari alla superficie; ridotto se i raggi arrivano obliqui rispetto alla superficie; nullo se sono paralleli alla superficie.

Riassumendo, l'illuminamento di una superficie dipende dall'intensità della sorgente, dalla distanza dalla sorgente, dall'angolo che forma con la superficie e dalla dimensione della superficie.
* Johann Heinrich Lambert (1728 - 1777), fisico, matematico e astronomo svizzero.
Luminanza
La luminanza fa riferimento alla luce riflessa o diffusa da una superficie.
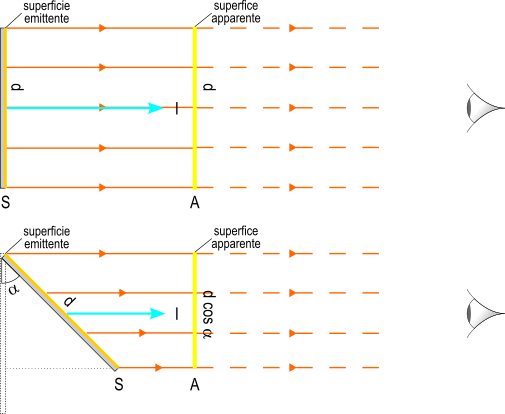
Una sorgente emette una radiazione luminosa che raggiunge una superficie. La luminanza L è la luce che una superficie estesa piana riflette o diffonde. Questa è data dal rapporto tra l'intensità luminosa I emessa da una superficie estesa piana verso l'osservatore e la superficie apparente di area A emessa dalla superficie in direzione dell'osservatore.
Per superficie apparente si intende la proiezione ortogonale dell'area su un piano normale alla direzione di emissione.
Anche in questo caso vale la legge di Lambert, poiché noi vediamo solo la componente perpendicolare alla direzione dell'osservatore del flusso luminoso:
cos α è il coseno dell'angolo compreso tra l'osservatore e l'asse della superficie che emette luce.
Se α = 0 la formula diventa quella precedente.
La luminanza dipende quindi dalla posizione dell'osservatore rispetto alla superficie emittente e quindi quanto più piccola è la superficie apparente, tanto maggiore è la luminanza che l'occhio percepisce.
L'unità di misura nel SI è il nit, corrispondente a 1 cd per 1 m2, oppure lo stilb (cd/cm2) o ancora, il lambert, che però non appartiene al SI.

