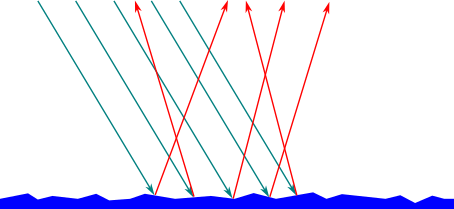
In questa pagina proponiamo i fenomeni ottici che considerano la luce come un fascio di raggi luminosi uscenti da una sorgente, che si propagano in linea retta.
Riflessione
Abbiamo già avuto modo in più occasioni di incontrare fenomeni di riflessione. Facciamo qui un riassunto delle caratteristiche principali.
Qualsiasi superficie levigatissima è in grado di riflettere la luce; tale superficie si chiama specchio. Esistono specchi di varie forme: piani, sferici, la cui superficie riflettente può essere quella interna (concavo) o quella esterna (convesso) e quelli parabolici, ugualmente concavi o convessi. Quelli di uso comune sono costituiti da un vetro, metallizzato con argento, alluminio o piombo nella parte posteriore.
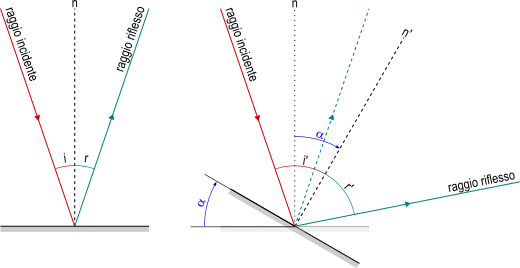
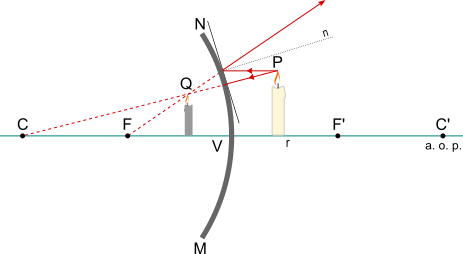
La legge della riflessione afferma che [1] a ogni raggio incidente su una superficie riflettente corrisponde un raggio riflesso, che inizia nel punto dove finisce il primo (punto di incidenza P).
La retta perpendicolare al piano della superficie riflettente (o al piano tangente, se è curva) nel punto di incidenza è la normale di incidenza (n). Gli angoli formati con la normale di incidenza sono rispettivamente angolo di incidenza e angolo di riflessione
.
Il piano a cui appartiene il primo angolo è il piano d'incidenza.
[2] Il raggio riflesso corrispondente a un raggio incidente appartiene al piano di incidenza e forma un angolo di riflessione uguale a quello di incidenza:

Il raggio incidente e quello riflesso sono tra loro simmetrici e da questo ne deriva che i due cammini ottici nella riflessione sono tra loro invertibili (Principio di reversibilità).
Specchio piano
I raggi riflessi formano in una data regione dello spazio un'immagine della sorgente luminosa.
Uno specchio piano è costituito da una superficie perfettamente piana.
Una sorgente S (punto-oggetto) emette raggi divergenti che incidono su uno specchio piano. Questi danno origine a raggi riflessi, ugualmente divergenti, i cui prolungamenti al di là dello specchio si incontrano in un punto S' (punto-immagine) simmetrico di S rispetto al piano riflettente: .
L'immagine S' della sorgente S è virtuale e i raggi riflessi sembrano emessi da una sorgente posta dietro allo specchio, ma non provengono realmente dall'immagine. L'immagine virtuale si forma nel punto di incontro dei prolungamenti divergenti dei raggi riflessi.

Per costruire geometricamente l'immagine, si tracciano due raggi divergenti da un punto dell'oggetto sorgente S, si disegnano i raggi riflessi e si prolungano dietro lo specchio.
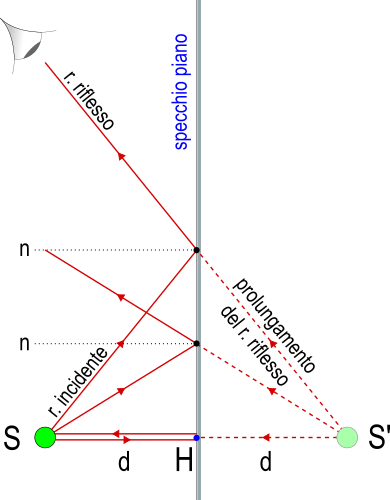
L'immagine riflessa da uno specchio piano:
- è virtuale in quanto non esiste, ma deriva dal prolungamento dei raggi divergenti riflessi;
- appare alla stessa distanza dallo specchio di quella dell'oggetto reale;
- presenta le stesse dimensioni dell'oggetto che si riflette;
- è simmetrica, rispetto a quella reale;
- è dritta verticalmente;
- è invertita orizzontalmente.
Per costruire l'immagine riflessa di un oggetto esteso si procede come indicato sopra, trattandolo come un insieme di punti, la cui immagine si ricava da ciascun punto. Come si vede nella figura, abbiamo usato due raggi che partono da due estremi.

Per riflettere una figura intera non è necessario avere uno specchio della stessa misura ma è sufficiente la metà della figura, indipendentemente dalla distanza cui questa si pone.

Se viene fatto ruotare uno specchio piano di un determinato angolo α, mantenendo fisso il raggio incidente, il raggio riflesso ruota di un angolo doppio 2α:
r' = 2r
Specchio sferico concavo
Lo specchio sferico concavo deriva dalla sezione di una sfera e la superficie riflettente è quella interna.
In esso riconosciamo il centro di curvatura C, avente il raggio di curvatura r (segmento ), il vertice V che è il punto al centro della calotta; la retta passante tra C e V si chiama asse ottico principale, mentre ogni altra retta passante per C è detta asse ottico secondario; l'apertura α dello specchio è l'angolo
compreso tra i due assi ottici secondari complanari più esterni
e
.
La normale n è la perpendicolare al piano tangente alla superficie nel punto di incidenza.

Poniamo un oggetto abbastanza lontano dal centro di curvatura.
Da un punto (punto-oggetto) posto sull'asse ottico principale partono dei raggi incidenti sullo specchio concavo.
(1) Se sono abbastanza vicini all'asse ottico, i raggi riflessi convergono in un punto (punto-immagine), dal quale poi proseguono divergendo.

(2) Se i raggi incidenti sono paralleli all'asse ottico principale, cioè l'oggetto è posto all'infinito, danno origine a raggi riflessi che passano tutti approssimativamente per un punto F, detto fuoco, che è il punto medio tra V e C.
La distanza tra il fuoco F e il centro dello specchio V è la distanza focale f; poiché il fuoco è approssimativamente il punto medio tra il centro di curvatura e il centro dello specchio:

Poiché tra i raggi paralleli solo quelli più centrali si riflettono nel fuoco, gli altri incontrano l'asse ottico principale in punti compresi tra F e V. Complessivamente i raggi riflessi si incontrano su una superficie curva chiamata caustica di riflessione.

(Clicca per un'immagine alternativa)
Come per gli specchi piani vale il principio di reversibilità dei cammini ottici, perciò i raggi incidenti che partono dal fuoco sono riflessi come raggi paralleli.
(3) Nel caso in cui il raggio incidente passi per C, questo si riflette su se stesso.
(4) Per i raggi che incidono sul vertice, il raggio riflesso è simmetrico rispetto all'asse ottico principale.

Le immagini di uno specchio sferico concavo non sono perfettamente nitide perché a un fascio di raggi incidenti omocentrici (con lo stesso centro) corrisponde un fascio di raggi riflessi solo approssimativamente omocentrico perché non convergono esattamente sul fuoco (questo fenomeno si chiama aberrazione sferica), mentre in uno specchio piano i raggi riflessi sono omocentrici. Le immagini sono tanto più nitide quanto più piccolo è l'angolo α di apertura dello specchio e quanto meno sono inclinati i raggi incidenti rispetto all'asse ottico principale.
Le immagini sono reali perché formate da un insieme di raggi che provengono realmente da un punto-oggetto e non sono quindi dei prolungamenti geometrici. Nelle immagini reali i raggi sono convergenti e si intersecano effettivamente in un punto-immagine; queste possono essere raccolte da uno schermo posto a un'opportuna distanza dallo specchio.
Nella figura sotto abbiamo un esempio di costruzione grafica di un'immagine ottenuta dalla riflessione di un oggetto su uno specchio sferico concavo.
Per la costruzione geometrica delle immagini, tra gli infiniti raggi incidenti che partono dal punto-oggetto se ne scelgono due di cui si conosca il percorso: parallelo, passante per C o passante per F.
Abbiamo usato il raggio passante per il centro e quello parallelo, al posto del quale si può usare il raggio passante per il fuoco (blu tratteggiato).
L'immagine è reale, ma visibile solo con uno schermo, capovolta e rimpicciolita.

Si tratta di uno dei casi che si possono presentare; gli altri sono riassunti nella tabella. L'immagine prodotta dipende dalla posizione dell'oggetto rispetto allo specchio.
| POSIZIONE OGGETTO | POSIZIONE IMMAGINE | IMMAGINE | COSTRUZIONE |
|---|---|---|---|
| P = ∞ | F | puntiforme sul fuoco * | 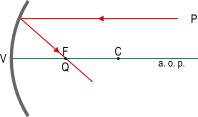 |
| P > r | F < Q < C | reale, capovolta, rimpicciolita, posta tra il fuoco e il centro. | 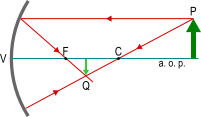 |
| P = r | Q = r | reale, capovolta, identica, posta nel centro. |  |
| F < P < r | Q > r | reale, capovolta, ingrandita, posta oltre il centro. | 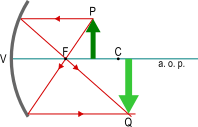 |
| P = F | Q = ∞ | immagine all'infinito perché i raggi sono paralleli. |  |
| P < F | Q < 0 | virtuale, diritta, ingrandita, posta oltre lo specchio. | 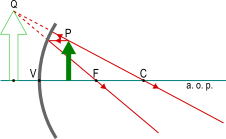 |
* Con l'oggetto posto all'infinito i raggi incidenti si considerano tutti paralleli all'a. o. p. e i raggi riflessi convergono tutti sul fuoco
F
reale.
Legge dei punti coniugati
In uno specchio sferico concavo di piccola apertura, a raggi incidenti emessi da un punto-oggetto P corrispondono raggi riflessi che convergono in un punto-immagine Q.
I punti P e Q sono chiamati punti coniugati. Se P si trova sull'asse ottico principale, anche Q si trova su a. o. p e se è posto all'infinito (raggi incidenti paralleli) il punto coniugato è il fuoco F.
Considerando l'a. o. p. come un asse delle ascisse, con verso positivo dal lato della concavità (per convenzione, le distanze dei punti dal vertice che si trovano davanti allo specchio sono positive e negative quelle dei punti che sono dietro lo specchio), r il raggio di curvatura e p e q le ascisse di P e Q, si dimostra (ma non lo faremo) che esiste tra p, q, e r la relazione:
Poiché la distanza focale f = r/2, la relazione diventa:

Ricordiamo che in uno specchio sferico concavo:
- p > 0 perché l'oggetto è sempre davanti allo specchio (oggetto reale);
- se q > 0 l'immagine è reale davanti allo specchio, se q < 0 l'immagine è virtuale dietro lo specchio;
- f > 0 ( f e r sono positivi se il centro di curvatura è davanti allo specchio).
Con la legge dei punti coniugati possiamo stabilire dove si forma l'immagine riflessa da uno specchio concavo conoscendo la posizione di un oggetto posto sull'a. o. p., oppure ricavare la posizione dell'oggetto conoscendo la distanza della sua immagine riflessa dallo specchio.
Ingrandimento
Nei paragrafi precedenti abbiamo parlato di ingrandimento e rimpicciolimento delle immagini riflesse.
In maniera più specifica, l'ingrandimento è il rapporto tra le dimensioni dell'immagine e quelle dell'oggetto e si indica con G.
Si può dimostrare, ma anche in questo caso non lo faremo, che la relazione che esprime l'ingrandimento è:
Secondo il valore di G, l'immagine è:
- G > 0: capovolta - reale
- G < 0: dritta - virtuale
- 0 < |G| < 1: rimpicciolita (anche se si chiama ancora “ingrandimento”)
- |G| = 1: identica
- |G| > 1: ingrandita
* Si è usato il valore assoluto perché l'ingrandimento può anche essere negativo e questo si verifica quando l'immagine è virtuale.
L'ingrandimento si può anche esprimere in funzione della distanza focale:
Specchio sferico convesso
Nello specchio sferico convesso la superficie riflettente è quella esterna.
Quanto detto per lo specchio sferico concavo vale anche per quello convesso, però il centro di curvatura C si trova dalla parte opposta rispetto alla superficie riflettente, l'asse ottico principale è rivolto verso la convessità, il fuoco F è virtuale e perciò è sempre negativo.
La distanza focale f anche in questo caso è la metà del raggio di curvatura, ma ha segno negativo:

Negli specchi sferici convessi le immagini sono sempre virtuali, diritte e rimpicciolite, poste tra il vertice dello specchio e il fuoco, per qualsiasi posizione dell'oggetto purché non sia all'infinito. In questo caso i raggi incidenti arrivano paralleli all'a. o . p. e quelli riflessi divergono dallo specchio, come nella figura sopra, e i loro prolungamenti si incontrano nel punto-immagine F', che è un fuoco virtuale.
Vediamo un esempio di costruzione geometrica dell'immagine.
Il raggio che parte dal punto-oggetto P, parallelo all'asse ottico principale, si riflette secondo le leggi già viste; il suo prolungamento passa per il fuoco F. Il cammino ottico è naturalmente invertibile.
Un secondo raggio che parte da P è prolungato fino al centro C; questo è riflesso lungo la stessa direzione.
La convergenza di questi due raggi si ha in Q, che è il punto-immagine.
In questo caso l'oggetto si trova dalla parte opposta rispetto alla superficie riflettente dello specchio e l'immagine ottenuta è sempre virtuale perché deriva dal prolungamento dei raggi, diritta e rimpicciolita, qualsiasi sia la posizione dell'oggetto davanti allo specchio.
Nel caso in cui l'oggetto sia posto all'infinito, l'immagine virtuale si forma nel fuoco dello specchio.
In uno specchio sferico convesso di piccola apertura, con raggi incidenti emessi da un punto-oggetto P, assumendo a. o. p. come asse delle ascisse e verso positivo dalla parte dove è rivolta la superficie riflettente, l'ascissa di C è -r e di F è -f, vale la medesima legge dei punti coniugati vista in precedenza, solo che la distanza focale è negativa:

In uno specchio sferico convesso, quindi:
- p > 0 perché l'oggetto è sempre davanti allo specchio;
- q < 0 l'immagine è sempre virtuale;
- f < 0.
L'ingrandimento G è sempre negativo e minore di 1 perché le immagini virtuali sono sempre rimpicciolite.
Il vantaggio di questi specchi è di dare un'immagine rimpicciolita su una porzione ampia dello spazio circostante, perciò è impiegata negli specchi retrovisori delle auto e in quelli stradali.
Specchio parabolico
Lo specchio parabolico deriva dalla rotazione di una parabola attorno al proprio asse.
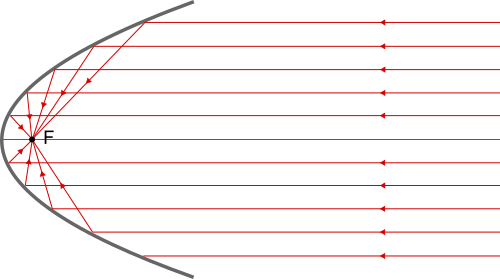
Come per lo specchio sferico, lo specchio parabolico può essere concavo o convesso. A differenza dei precedenti, però, il fuoco F coincide perfettamente con il fuoco geometrico della parabola. Il fuoco, come nei casi precedenti, è il punto in cui convergono i raggi riflessi dei raggi incidenti paralleli all'asse ottico principale (nella figura non sono disegnati i prolungamenti oltre il fuoco dei raggi riflessi).
Diffusione
Un'altra proprietà che abbiamo già incontrato è la diffusione, che è la riflessione prodotta da superfici che non sono perfettamente levigate. In questo caso i raggi riflessi assumono direzioni e inclinazioni varie.