Gli effetti relativistici secondo Einstein sono:
- dilatazione dei tempi,
- contrazione delle lunghezze,
- relatività della simultaneità.
I primi due li abbiamo già visti, affrontiamo ora il terzo.
Concetto di simultaneità
Tutti sanno che se due eventi sono contemporanei avvengono nello stesso istante. Se accadono nello stesso luogo, la simultaneità è un dato immediato, la cui determinazione non implica nessuna difficoltà. Quando invece si tratta di eventi che accadono in uno spazio-tempo differente, non è possibile affermare la loro simultaneità.
Prendiamo in considerazione un sistema in cui siano valide le leggi della meccanica classica.
Nei punti A e B esistono due orologi tra loro identici. Un osservatore posto in A misura con il suo orologio un evento accaduto nelle vicinanze, cioè la posizione delle lancette dell'orologio è simultanea all'evento in questione. Un altro osservatore, nel punto B, misura un evento nelle sue vicinanze con il suo orologio identico.
Conosco il tempo locale in A e in B, ma non so se gli eventi sono contemporanei o meno. Con la meccanica classica si pensava di poter verificare la contemporaneità degli eventi inviando un particolare segnale luminoso o elettrico, ritenendo istantanea la propagazione dell'informazione.
Secondo i principi della relatività di Einstein, invece, non è possibile tale verifica perché la luce ha una velocità elevatissima, costante, ma finita, perciò la propagazione delle informazioni non è istantanea. Devo, infatti, tenere conto della distanza e del tempo impiegato dal segnale per raggiungere l'osservatore. I due osservatori, quindi, calcoleranno in maniera diversa il tempo impiegato dal segnale per giungere da un punto ad un altro, perciò non è possibile stabilire la simultaneità dei due eventi, non essendoci un sistema privilegiato che debba considerarsi come il vero e assoluto.
I due orologi dell'esempio precedente erano posti in posizione fissa nei rispettivi punti. Vediamo ora il caso in cui uno degli osservatori sia in movimento.
Se un osservatore giudica simultanei due eventi del sistema di cui fa parte, per un altro osservatore, in moto rettilineo uniforme rispetto al primo, non sono più tali: la simultaneità è un concetto relativo all'osservatore, cioè al sistema di riferimento. Si tratta di un corollario necessario del postulato dell'invarianza della velocità della luce rispetto a un osservatore qualunque in qualsiasi sistema di riferimento.
L'animazione seguente ci mostra come gli eventi A, B e C appaiano simultanei a un osservatore in quiete, ma non lo sono più quando è in moto rettilineo uniforme.

(Crediti:
Acdx
- Self-made, based on
Image:Relativity_of_Simultaneity.svg
, source code:
en:User:Acdx/Relativity_of_Simultaneity_Animation
- CC BY-SA 4.0)
Chiariamo questo concetto - differenza tra la percezione di un osservatore in quiete e uno in moto rettilineo uniforme - con un disegno.
Dalla Terra un osservatore in quiete vede esplodere contemporaneamente due supernove A e B, quindi percepisce i due eventi come simultanei.*
* È superfluo, ai fini dell’esempio, specificare che i due eventi sono realmente simultanei solo se equidistanti dall’osservatore. Potrebbero anche non essere simultanei e percepiti come tali se l’osservatore non è equidistante dai due eventi, ma sarebbe un esempio diverso da quello che stiamo proponendo e non chiarirebbe l’animazione, come è invece nostra intenzione.
Un altro osservatore, che si trova in viaggio su un'astronave con moto rettilineo uniforme (il sistema di riferimento è quindi diverso dal precedente), dopo aver superato la stella A, vede esplodere la stella B verso la quale si sta avvicinando. Poco dopo vede dietro di sé esplodere anche la stella A. L'astronauta vede la luce dell'esplosione di B prima di quella di A, perciò ne deduce che nel sistema di riferimento dell'astronave i due eventi non siano simultanei. Questo accade perché l'astronave si avvicina alla sorgente di luce B, mentre si allontana dalla sorgente A. Ritorneremo su questo aspetto nella prossima pagina.
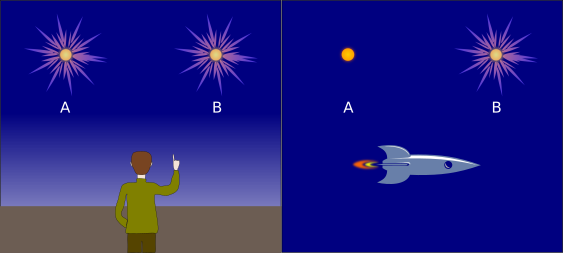
Come si voleva dimostrare, i due osservatori, trovandosi in due sistemi di riferimento diversi, percepiscono in modo differente i due eventi e non è possibile stabilire quale dei due sia nel vero.
Per completare l'esposizione proponiamo un esperimento mentale di Einstein.
Consideriamo la carrozza di un treno di lunghezza L, misurata quando è ferma, una ragazza ferma sulla banchina della stazione e il suo ragazzo dentro la carrozza. Entrambi gli osservatori sono equidistanti dalle estremità.

Supponiamo che, quando il treno è ancora fermo, due fulmini cadano contemporaneamente e colpiscano rispettivamente i punti A e B della carrozza, che corrispondono ai punti A e B della banchina. Entrambi gli osservatori sono concordi nel ritenere che i due eventi si siano verificati simultaneamente.
Immaginiamo ora che il treno sia in movimento con velocità costante v verso la direzione di B, rispetto all'osservatrice a terra (il sistema di riferimento inerziale è la banchina). Proprio quando i due ragazzi si trovano esattamente l'uno di fronte all'altro, due fulmini colpiscono le estremità della carrozza.
Supponiamo anche che per la ragazza siano simultanei i fulmini che colpiscono le estremità della carrozza e quindi li percepisce contemporaneamente. Il ragazzo (sistema di riferimento è il treno in moto), invece, afferma che è caduto prima il fulmine in B. Questo si spiega perché l'osservatore si sta muovendo verso B e si sta allontanando da A e quindi il raggio di luce emesso nel punto B raggiunge il ragazzo prima di quello in A.
Il concetto che si ricava dall'esempio è che gli eventi che sono simultanei per un osservatore in quiete, non lo sono per l'osservatore in movimento rispetto a quello in quiete, cioè gli eventi che sono simultanei rispetto alla banchina non sono simultanei rispetto al treno.
Va anche per la situazione contraria: il ragazzo seduto fermo sulla carrozza del treno in movimento, che per lui è ferma, vede la banchina e la ragazza scorrere verso A. Se i 2 fulmini cadono sulla banchina contemporaneamente, la ragazza li percepisce simultanei, ma il ragazzo vede prima quello in B.
Sono possibili altre due combinazioni: lampi simultanei per il ragazzo e due sistemi di riferimento, il treno e la banchina.
Ne concludiamo che ogni volta che si verificano due eventi, entro il tempo che impiega la luce a compiere il tragitto che li separa, l'ordine in cui si verificano non è definito: esso dipende dalla velocità dell'osservatore e quindi ogni osservatore (sistema di riferimento) ha il suo tempo proprio.
Riprendiamo il paradosso
Tornando al nostro paradosso, l'evento “Partenza dell'astronave” avviene simultaneamente per Arturo e Basilio, che si trovano vicini e nello stesso sistema di riferimento terrestre nel 3000. Lo stesso vale per l'evento “Ritorno dell'astronave”, nel 3020.
Non è così però per l'evento “Basilio arriva sulla Stella”.
Per Basilio gli eventi “Partenza dell'astronave” e “Basilio arriva sulla Stella” sono rispettivamente simultanei, cioè li vede subito nelle stesse coordinate di spazio-tempo, trovandosi all'interno dell'astronave.
Per Arturo, invece, non lo sono perché li vede in due punti diversi del suo sistema di riferimento e perciò deve aspettare il tempo che la luce impiega a coprire la distanza Stella-Terra.
Questa asimmetria, come vedremo nel diagramma, determina la differenza temporale misurata dai due gemelli tra gli eventi “Partenza dell'astronave” e “Ritorno dell'astronave”.
Il digramma di Minkowski
Vediamo con il diagramma di Minkowski, e lavorando con le linee di simultaneità - rette parallele all'asse x -, quali sono gli eventi simultanei per ciascun gemello. Sono simultanei gli eventi che hanno la stessa coordinata temporale in un dato sistema e perciò non si mantiene la simultaneità tra due eventi le cui coordinate sono calcolate in sistemi inerziali diversi.
L'asse temporale ct rappresenta un oggetto fermo in una determinata posizione e il suo trascorrere del tempo, dove x = costante.
L'asse spaziale x e le rette a esso parallele rappresentano l'insieme degli eventi simultanei ad un dato evento preso come riferimento, dove ct = costante.
La linea oraria della luce è inclinata di 45°.

Nel grafico sopra, gli assi di colore nero rappresentano lo spazio-tempo terrestre in cui Arturo non si muove: x = 0 e gli eventi avvengono tutti lungo l'asse ct (si muove solo nel tempo).
La linea verde è la linea oraria della Stella, verticale perché si presume fissa (quindi parallela a ct), con x = 8 a.l.
Gli assi in rosso rappresentano il sistema di riferimento dell'astronave nel viaggio di andata verso la Stella. Sono inclinati perché l'astronave è in movimento: Basilio si muove nell'intervallo temporale 3000 - 3006.
Gli assi in blu si riferiscono al viaggio di ritorno di Basilio (3006 - 3012).
Basilio è in movimento perciò bisogna trovare trovare i nuovi assi: ct', x' per l'andata e ct'', x'' per il ritorno.
Una volta conosciuta l'inclinazione di ct' - ricordiamo che dipende dalla velocità ( in questo caso 0,8 c) -, si può tracciale la retta x', sapendo che l'angolo con la linea della luce è identico a quello della retta ct' con la luce. Per determinare le coordinate di un evento nel nuovo sistema di riferimento basta tracciare delle rette parallele a ct' e x' e trovare i punti di intersezione con questi assi. Lo stesso vale per ct'', x''.
I nuovi assi non sono più ortogonali e questo dipende dalla trasformazione di Lorentz.
Il tutto è ben rappresentato nell'animazione sottostante.

(Crediti:
Lylvic CC BY-SA 4.0
)
Viaggio di andata dal punto di vista terrestre
L'evento “Basilio arriva alla Stella” si ha quando l'orologio di Arturo segna 3010, ma anche l'orologio della Stella segna 3010 perché la Terra, la Stella e lo spazio tra i due appartengono al sistema di riferimento inerziale terrestre, mentre l'astronave e Basilio fanno parte del sistema di riferimento inerziale dell'astronave.
L'orologio di Basilio segna, invece, 3006 (dilatazione temporale vista in precedenza) ed è simultaneo al 3010 terrestre (linea viola parallela a x del sistema ct, x), dove v = 0.
L'astronave però si muove nello spazio-tempo, perciò serve un nuovo sistema ct', x' per l'andata (in rosso).
Possiamo tracciare infinite rette parallele a x', ma a noi interessa quella passante per il 3006. Questa è la linea di simultaneità che incrocia l'asse ct nel 3003,6 terrestre.
L'evento “Basilio incontra la Stella” (3006) è quindi simultaneo dell'evento in cui l'orologio di Arturo, nel sistema di riferimento di Basilio, segna 3003,6 a una distanza di -4,8 a.l.
L'orologio appare rallentato (6 × 0,6 della dilatazione temporale) perché l'astronave si sta allontanando dalla sorgente dei fotoni terrestri (si veda l'esempio delle supernove proposto sopra).
Secondo Arturo, per lui sono passati 3,6 anni e per Basilio 6.
Viaggio di andata dal punto di vista dell'astronave
Quando Basilio è nei pressi della Stella, il suo orologio segna 3006, l'orologio della Stella segna 3010 e l'orologio di Arturo lo “vede” indicare 3003,6.
L'orologio di Arturo e della Stella non sono più sincronizzati, essendoci una differenza di 6,4 anni.
Da questo deduce che l'orologio di Arturo ritarda e quindi:
Secondo Basilio, per lui sono passati 6 anni e per Arturo 3,6
Viaggio di ritorno
Arrivato alla Stella, Basilio fa un'inversione a U, presumendo in un tempo trascurabile, cambiando sistema di riferimento, che ora è ct'', x'' (in blu). In esso l'orologio terrestre risulta in anticipo di 6,4 anni rispetto a quello della Stella.
Nel nuovo sistema di riferimento, non solo cambia la linea oraria, che ora incontra la linea oraria terrestre nel punto con data 3020 (evento “Ritorno dell'astronave”), ma anche la linea di simultaneità, che ora incrocia l'asse ct nel 3016,4.
L'orologio terrestre questa volta sembra accelerare e questo perché l'astronave si sta avvicinando alla sorgente dei fotoni terrestri.
Ora possediamo tre eventi terrestri, 3003,6, 3010, 3016,4, simultanei all'evento “Basilio arriva alla Stella” e non è possibile stabilire quale sia quello effettivo perché dipende dal sistema di riferimento: è la relatività della simultaneità.
La variazione di sistema di Basilio, per lui è istantanea, ma sulla Terra sono trascorsi 3016,4 - 3003,6 = 12,8 anni. Questi sono gli anni mancanti nella vita di Basilio nel sistema di riferimento dell'astronave.
Questo cambio di riferimento provoca una differenza di tempo - e quindi una differenza di invecchiamento tra i gemelli - dovuta alla non conservazione della simultaneità.
Dopo l'inversione c'è il viaggio di ritorno:
Secondo Arturo, per lui sono passati 3,6 anni e per Basilio 6.
Secondo Basilio, per lui sono passati 6 anni e per Arturo 3,6
Ancora una volta concordano sugli intervalli temporali.
In conclusione:
Per Arturo sono dunque trascorsi 3,6 (viaggio di andata del gemello) + 12,8 (tempo durante l'inversione) + 3,6 (viaggio di ritorno del gemello) = 20 anni.
Per Basilio sono invece trascorsi 6 (viaggio di andata) + 0 (tempo durante l'inversione) + 6 (viaggio di ritorno) = 12 anni.
Quando i due gemelli si incontrano sono concordi nell'affermare che effettivamente Basilio è più giovane di Arturo indipendentemente dal sistema di riferimento, pertanto il paradosso non esiste.

