Una descrizione più accurata dell'argomento si trova nella sezione di fisica.
La legge isoterma di Boyle-Mariotte (1662)

A temperatura costante, il volume occupato da un gas è inversamente proporzionale alla pressione esercitata su di esso.
V = k · 1/ P
P V = k

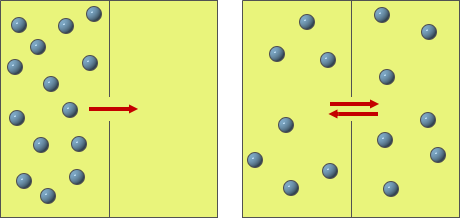
Essendo le particelle puntiformi e lo spazio tra esse molto ampio, le particelle possono avvicinarsi con la compressione, però, in questo caso, essendoci meno spazio a disposizione, aumentano gli urti contro le pareti del recipiente e quindi la pressione.
Con l'aumento di pressione, il volume si riduce, ma non la sua massa, perciò diventa più denso.
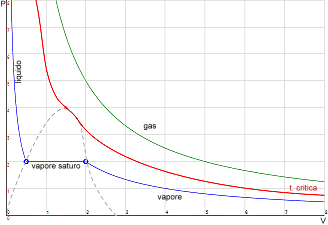
La temperatura critica Tc è la linea di demarcazione tra gas e vapore.
Sopra la temperatura critica il gas si comporta come gas ideale e graficamente abbiamo iperboli equilatere. La semplice compressione non liquefa il gas, ma occorre anche raffreddare.
Sotto la temperatura critica abbiamo il vapore, che per compressione diventa liquido. Infatti, compare un gradino nel grafico dove coesistono vapore e liquido e ad un certo punto tutta la massa diventa liquida e quindi incomprimibile.
Per ogni trasformazione isoterma è possibile calcolare la pressione o il volume secondo la relazione:
![]()
La legge isobara di Charles (1787) e la prima legge di Gay-Lussac
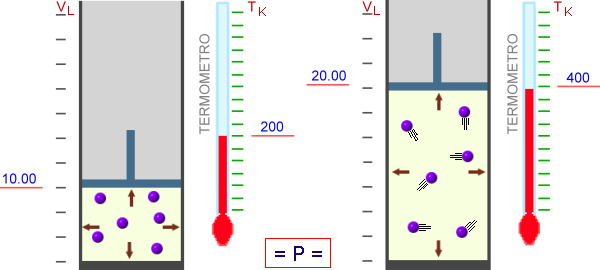
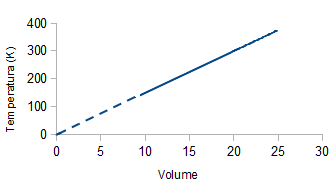
A pressione costante, il volume di un gas è direttamente proporzionale alla temperatura assoluta (Legge di Charles).
V = k T
V / T = k
All'aumentare della temperatura, le particelle aumentano la loro energia cinetica media e quindi la forza degli urti, che però viene compensata da una loro minore frequenza per l'aumento del volume.
La proporzionalità tra V e T deriva dalla prima legge di Gay-Lussac sulla dilatazione:
Per ogni aumento di un grado centigrado di temperatura, il volume aumenta di 1/273 rispetto al volume iniziale.
Vt = V0 (1 + α t)
dove α = 1/273 °C
Possiamo calcolare il volume o la temperatura di un gas in una trasformazione isobara con la relazione:
![]()
La seconda legge isocora di Gay-Lussac (1802)
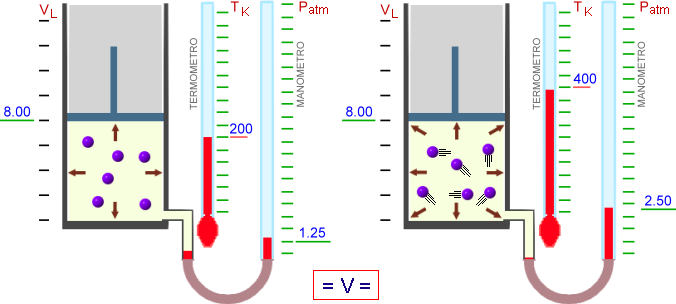
A volume costante, la pressione di un gas è direttamente proporzionale alla sua temperatura assoluta.
P = k T
P / T = k

All'aumentare della temperatura, le particelle aumentano la loro energia cinetica media ma, rimanendo il volume costante, aumenta il numero degli urti sulle pareti del recipiente e quindi la pressione.
Come visto per la prima legge di Gay-Lussac, per ogni aumento di un grado di temperatura, la pressione aumenta di 1/273 rispetto alla pressione iniziale.
Pt = P0 (1 + α t)
dove α = 1/273 °C
Analogamente alla legge precedente, possiamo calcolare la pressione o la temperatura di un gas, a volume costante, con la relazione:

Legge combinata dei gas
Le tre precedenti leggi mantengono costante un parametro mentre variano gli altri due. Combinandole insieme possiamo ottenere una relazione che verifica il comportamento di un gas quando si modificano le tre variabili.
P V / T = k
Perciò:
![]()
Il principio di Avogadro
Avogadro dimostrò sperimentalmente che il volume di un gas non dipende dalla sua natura ma solo dal numero di moli, e quindi di particelle.
Volumi uguali di gas diversi alle stesse condizioni di pressione e temperatura contengono lo stesso numero di molecole.

Volume molare
In base al principio di Avogadro, una mole di qualsiasi gas ideale alle condizioni standard occupa un volume (volume molare), determinato sperimentalmente, pari a 22,4 L.

Equazione di stato dei gas ideali
Secondo le quattro relazioni di proporzionalità presentate sopra, essendo il volume inversamente proporzionale alla pressione e direttamente proporzionale alla temperatura e al numero di moli, è stato confermato sperimentalmente che anche per il prodotto di queste variabili vale la medesima relazione.
V ∝ 1/P | V ∝ T | V ∝ n
V ∝ nT/P cioè PV ∝ nT
Per una mole di un gas ideale alle condizioni standard si può calcolare il valore della costante.
![]()
La costante universale dei gas ideali, indicata con R vale 0,0821 se la pressione è espressa in atmosfere, il volume in litri, la temperatura in Kelvin e la quantità di sostanza in moli.
Possiamo ora scrivere l'equazione di stato dei gas ideali:
P V = n R T
Legge delle pressioni parziali di Dalton (1882)
Gas di tipo diverso possono essere mescolati tra loro in tutte le proporzioni purché non ci siano reazioni chimiche tra loro.
In una miscela gassosa, la pressione parziale di un gas è la pressione che esso eserciterebbe se fosse da solo nel recipiente alla stessa temperatura e pressione.
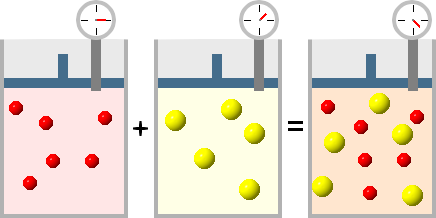
La pressione esercitata da una miscela gassosa è uguale alla somma delle pressioni parziali che esercitano i singoli componenti gassosi.
Ptot V = ntot R T
La diffusione
I gas, più rapidamente dei liquidi, diffondono facilmente e rapidamente nell'ambiente, grazie all'elevata velocità delle particelle, distribuendosi in modo uniforme.
A parità di temperatura, la diffusione è tanto più rapida quanto più sono leggere le particelle.